Here , we are going to use the property of linear pair . So , this property states that on any line , the sum of all angles formed by drawing other lines on the initial line is 180° or π radians .
__________________________
Coming back to the question , we are provided that ;
Now by property of linear pair , we have ;
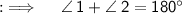
Putting the values ;
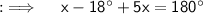
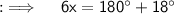
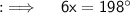
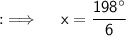
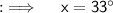
Now , we can find measures of
 &
&
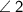 , by putting the value of x
, by putting the value of x

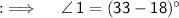
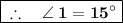

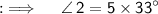
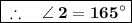
We are Done :D