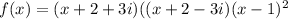Question

Using a given zero to a polynomial as a product of linear factors complex zeros

Answer 1

When we have a polynomial of higher degree bu we know some of its zeros, we can use synthetic division to factor the polynomial and solve the remaining factors.

We have apolynomial of fourth degree, and we know that 1 is a zero with multiplicity two, that is, the polynomial have two factors (x - 1), so it can be rewritten as:

`x^4-6x^3+22x^2-30x+13=(ax^2+bx+c)(x-1)(x-1)=(ax^2+bx+c)(x-1)^2`

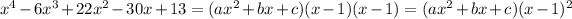
To find out the quadratic fator, we can do the synthetic division by 1 twice.

To do this, e start by writing 1 and the coefficients of the polynomial:

1 | 1 -6 22 -30 13

|

| 1

The leading coefficient was also copied to the last row. Now, we will do the following repeatedly:

- multiply the number on the last row of the column we are by the divisor "1" and put the result under the next coefficient (the column to the right).

- add the two rows of this next coefficient and put the result in the last row.

- repeat

So:

1 | 1 -6 22 -30 13

| 1

| 1 -5

1 | 1 -6 22 -30 13

| 1 -5

| 1 -5 17

1 | 1 -6 22 -30 13

| 1 -5 17

| 1 -5 17 -13

1 | 1 -6 22 -30 13

| 1 -5 17 -13

| 1 -5 17 -13 0

Now, the 4 first numbers in the last row are the coefficients of the polynomial that is the result, and the last is the remainder, which is zero because 1 is a zero of the original polynomial.

Now, we can rewrite the polynomial as:

`x^4-6x^3+22x^2-30x+13=(x^3-5x^2+17x-13)(x-1)`

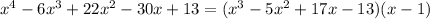
Now, we take this third degree polynomial and divide again by 1:

1 | 1 -5 17 -13

|

| 1

1 | 1 -5 17 -13

| 1

| 1 -4

1 | 1 -5 17 -13

| 1 -4

| 1 -4 13

1 | 1 -5 17 -13

| 1 -4 13

| 1 -4 13 0

Now, we can rewrite the third degree polynomial as:

`x^3-5x^2+17x-13=(x^2-4x+13)(x-1)`

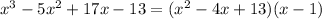
So, the original becomes:

`x^4-6x^3+22x^2-30x+13=(x^2-4x+13)(x-1)^2`

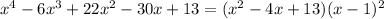
Now, to finish the factoring, we can find the zeros of the quadratic factor, which we can do by using the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(13)}}{2(1)}=\frac{-4\pm\sqrt[]{16-52}}{2} \\ x=\frac{-4\pm\sqrt[]{-36}}{2}=(-4\pm6i)/(2)=-2\pm3i \\ x_1=-2-3i \\ x_2=-2+3i \end{gathered}`

So, we can write the quadratic factor as:

`x^2-4x+13=(x-(-2-3i))(x-(-2+3i))=(x+2+3i)(x+2-3i)`

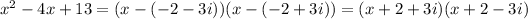
So, the original polynomial as a product of linear factors is:

`f(x)=(x+2+3i)((x+2-3i)(x-1)^2`