To find the length of the ladder we need to use the right triangle formed between the house, the ground, and the ladder.
We use the trigonometric function cosine, defined for an angle X as follows:
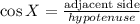
In this case, the known angle is:
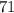
Thus, we have to find the adjacent side to the 71° angle, and the hypotenuse of the triangle:
We will call the hypotenuse "h" just for reference.
Using the known values of the adjacent side and the angle, the cosine is:
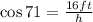
The hypotenuse h is the length of the ladder, so we solve for h in the previous equation:
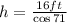
And solve the operations to find h (the length of the ladder):
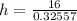
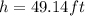
the length of the ladder is 49.14 ft.
Rounding the answer to the nearest tenth (1 decimal place):

Answer: 49.1 ft