The number of observations in the data is n = 10.
Determine the mean of the data.
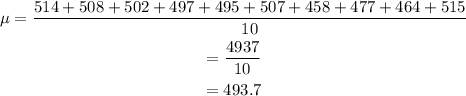
So mean of the data is 493.7.
Determine the sum of square difference between observation and mean.
![\begin{gathered} \sum ^n_(i\mathop=1)(x_i-\mu)^2=(514-493.7)^2+(508-493.7)^2+(502-493.7)^2+(497-493.7)^2 \\ +(495-493.7)^2+(507-493.7)^2+(458-493.7)^2+(477-493.7)^2+(464-493.7)^2+(515-493.7)^2 \end{gathered}]()
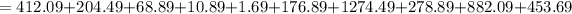
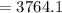
The formula for the standard deviation is,
![\sigma=\sqrt[]{(\sum ^n_(i=1)(x_i-\mu)^2)/(n-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/tezuas758cozpv4dmn6r2o0k68zpt2sc3k.png)
Substitute the value in the formula to determine the standard deviation of the data.
![\begin{gathered} \sigma=\sqrt[]{(3764.1)/(10-1)} \\ =\sqrt[]{(3764.1)/(9)} \\ =20.4507 \\ \approx20.45 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vpjao9pd6158ib4qqqu3tsp7qjw0tc8kqj.png)
Answer:
Mean: 493.7
Standard deviation: 20.45