Question

How do the lower quartiles of the two sets of data compare?

Answer 1

Step 1

The first quartile is the value separating the lower quarter and the higher three-quarters of the data set.

The first quartile is sorted by taking the median of the lower of a sorted set.

Find the lower quartile of Milton

Arrange the data in ascending order

`0,\: 54,\: 73,\: 85,\: 86,\: 89,\: 90,\: 91,\: 94,\: 95,\: 97`

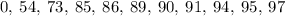
Take the lower half of the ascending set

`0,54,73,85,86`

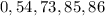
Hence, the lower quartile of Milton is 73

Step 2

Find the lower quartile of Makenzie

Arrange the data in ascending order

`84,\: 91,\: 92,\: 92,\: 93,\: 95,\: 97,\: 98,\: 98,\: 100,\: 100`

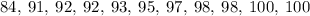
Take the lower half of the ascending set

`81,91,92,92,93`

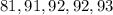
Hence the lower quartile of Makenzie = 92

The lower quartile of Milton is 73 and the lower quartile of Makenzie is 92. This means that the lower quartile of Makenzie is higher than the lower quartile of Milton and this is by (92-73)=19