Question

John wants to choose 4 of his friends to go to Disneyland with him. If he has 15 friends, in howmany ways can he choose 4 of them?

Answer 1

In this case, the order does not matter and we can not replace it.

Hence, we need to use a combination for this case.

The equation is given by:

`nCx=(n!)/(x!(x-n)!)`

Where n represents the total number of friends and x represents the number of the group.

Then,

n = 15 friends

x = choose 4 of them

Replacing:

`15C4=(15!)/(4!(15-4)!)`

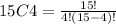
Simplify:

`\begin{gathered} 15C4=(15!)/(4!11!) \\ 15C4=1365 \end{gathered}`

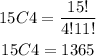
Hence, Jhon can choose them 1365 ways.

The correct answer is option d.