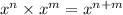The given expressions are

Consider the first expression
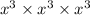
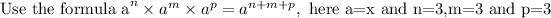
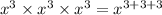
Adding 3,3 and 3, we get 9

Consider the second expression
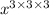
Multiplying 3,3 and 3, we get 27
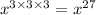
Equating both expressions as follows:
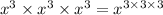
Substitute values, we get
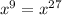
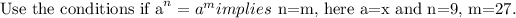
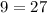
It is not true.
Hence the given two expressions are not equivalent.
The reason is it doesn't satisfy the following condition