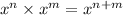Question

Is the expression x^3 X x^3 X x^3 equivalent to x^3X3X3 ? Why or why not?

Answer 1

The given expressions are

`x^3* x^3* x^3\text{ and }x^(3*3*3)`

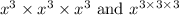
Consider the first expression

`x^3* x^3* x^3`
`\text{Use the formula a}^n* a^m* a^p=a^(n+m+p),\text{ here a=x and n=3,m=3 and p=3}`

`x^3* x^3* x^3=x^(3+3+3)`

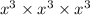
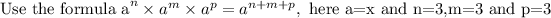
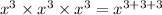
Adding 3,3 and 3, we get 9

`x^3* x^3* x^3=x^9`

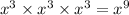
Consider the second expression

`x^(3*3*3)`

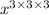
Multiplying 3,3 and 3, we get 27

`x^(3*3*3)=x^(27)`

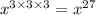
Equating both expressions as follows:

`x^3* x^3* x^3=x^(3*3*3)`

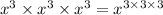
Substitute values, we get

`x^9=x^(27)`
`\text{Use the conditions if a}^n=a^mimplies^{}_{}\text{ n=m, here a=x and n=9, m=27.}`
`9=27`

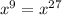
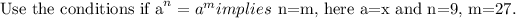
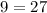
It is not true.

Hence the given two expressions are not equivalent.

The reason is it doesn't satisfy the following condition

`x^n* x^m_{}=x^(n+m)`