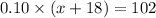Question

You need a 10% alcohol solution. On hand, you have a 120 mL of a 85% alcohol mixture. How much pure water will you need to add to obtain the desired solution?A) Write an equation using the information as it is given above that can be used to solve this problem. Use x as your variable to represent the amount of pure water you need to use.Equation: ________ You will need ____mL of pure waterto obtain ____mL of the desired 10% solution.

Answer 1

Here the mixture (or solution) contains alcohol and water.

Given that you have 85% alcohol mixture. It means that each 1 mL of the mixture will contain 0.85 mL of alcohol, and the remaining 0.15 mL of pure water.

So the amount of alcohol in 120 mL of mixture is calculated as,

`\begin{gathered} =120*0.85 \\ =102 \end{gathered}`

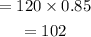
When 'x' mL of pure water is added to the solution, the total amount of water in the mixture becomes,

`\begin{gathered} =x+(120*0.15) \\ =x+18 \end{gathered}`

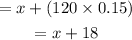
Since no alcohol is added, the amount of alcohol in the final mixture will remain same, that is, 102 mL.

Now, it is given that the concentration of the final mixture is 10%, So the amount of alcohol in the solution should be 10% of the total mixture,

`\begin{gathered} 0.10*(x+18+102)=102 \\ x+120=(102)/(0.10) \\ x+120=1020 \\ x=1020-120 \\ x=900 \end{gathered}`

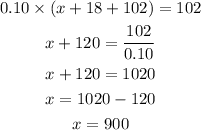
Thus, you need to add 900 mL of pure water in order to have 10% alcohol solution.

And the equation used to solve this problem is,

`0.10*(x+18)=102`