Here the mixture (or solution) contains alcohol and water.
Given that you have 85% alcohol mixture. It means that each 1 mL of the mixture will contain 0.85 mL of alcohol, and the remaining 0.15 mL of pure water.
So the amount of alcohol in 120 mL of mixture is calculated as,

When 'x' mL of pure water is added to the solution, the total amount of water in the mixture becomes,
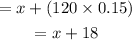
Since no alcohol is added, the amount of alcohol in the final mixture will remain same, that is, 102 mL.
Now, it is given that the concentration of the final mixture is 10%, So the amount of alcohol in the solution should be 10% of the total mixture,
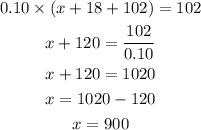
Thus, you need to add 900 mL of pure water in order to have 10% alcohol solution.
And the equation used to solve this problem is,
