We are given that company A charges $50 per hour and a fixed fee of $150. The total cost "Ca" is then given by the product of the number of hours "t" by the fee per hour plus the fixed fee. This is written mathematically as:
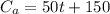
Company B charges $25 per hour and a fixed fee of $250. If Cb is the cost for company B, then we have:

To determine the number of hours "t" for when the cost is the same, then we need to set both costs equal:
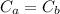
Now we substitute the expression for each cost:

Now we solve for "t", first by subtracting "25t" from both sides:
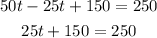
Now we subtract 150 from both sides:
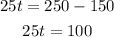
Now we divide both sides by 25:
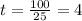
Therefore, the cost for both companies is the same after 4 hours.
To graph the functions we need to have into account that both equations represent lines since they are of the form:

Where "m" is the slope and "b" is the y-intercept. Since the equations are lines we need to determine two points in each one of them.
Let's take the equation for compañy "a" and we replace the value t = 0, we get:
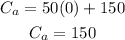
Therefore, the point (0, 150) is in the line for company "a". Now we substitute t = 1, we get:
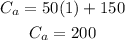
Therefore, the point (1, 200) is also on the line. Now we plot the two points and join them with a line to get the graph. It looks like this:
Now we use the same procedure for company B and we get the following graph:
We notice that the interception point between the lines is the point where the costs are the same.