Answer:
Option B is correct
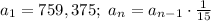
Explanations:
The nth term of a geometric sequence is given as:

where:
a is the first term
r is the common ratio
If two terms in a geometric sequence are a₅ = 15 and a₆ = 1, then;
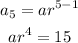
Similarly;

Take the ratio of both expressions to get the common ratio "r"

The standard recursive function is given as:
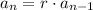
Substitute the value for the common ratio to have;

To get the first term a₁, we will use the equivalent nth term of the sequence above
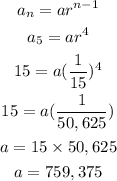
Hence the first term of the sequence is 759,375