Answer:
t = 8 seconds
Explanation:
Given the equation:
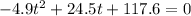
First, multiply all through by 10 in order to change the decimals to whole numbers as it is easier to work with whole numbers.
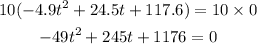
Next, factor out 49.
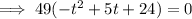
Divide both sides by 49:
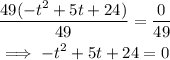
So, we have succeeded in reducing the initial equation given to the form above.
Next, factorize to solve for t.
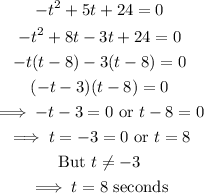
The ball will hit the ground after 8 seconds.