Question

I need this problem for my prep guide explained and answered

Answer 1

The standard form of the equation of a hyperbola with

center (h, k) and transverse axis parallel to the y-axis is

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

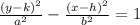
The coordinates of the foci are

`(h,k\pm c)`

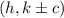
Where c is

`c^2=a^2+b^2`

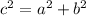
Since the given equation is

`((y-1)^2)/(9)-((x-3)^2)/(16)=1`

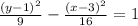
Compare it with the form above, then

`\begin{gathered} h=3 \\ k=1 \\ a^2=9 \\ b^2=16 \end{gathered}`

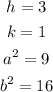
Let us find c by using the rule above

`\begin{gathered} c^2=9+16 \\ c^2=25 \\ c=\pm\sqrt[]{25} \\ c=\pm5 \end{gathered}`

Substitute the values of h, k, c in the coordinates of the foci above

`\begin{gathered} (3,1+5),(3,1-5) \\ (3,6),(3,-4) \end{gathered}`

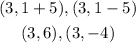
The coordinates of the foci are (3,6) and (3,-4)