The standard form of the equation of a hyperbola with
center (h, k) and transverse axis parallel to the y-axis is
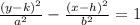
The coordinates of the foci are

Where c is

Since the given equation is
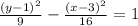
Compare it with the form above, then
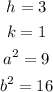
Let us find c by using the rule above
![\begin{gathered} c^2=9+16 \\ c^2=25 \\ c=\pm\sqrt[]{25} \\ c=\pm5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w5ttbw8am0emuel9bbck84bz1cy65eaxyh.png)
Substitute the values of h, k, c in the coordinates of the foci above
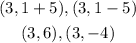
The coordinates of the foci are (3,6) and (3,-4)