Given
Initial velocity:
36 ft/s
Initial height:
0 ft
Vertical motion model:
h(t) = -16t^2 + ut + s
v = initial velocity
s = is the height
Procedure
We are going to use the model provided for the vertical motion.
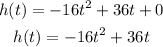
We know that at the maximum height the final velocity is 0.
Then we will use the following expression to calculate the maximum height:
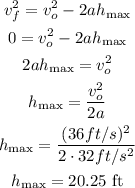
Now for time:
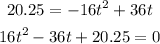
Solving for t,
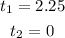
The total time the kangaroo takes in the air is 2.3s.