1.
Original function
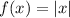
Left 3 units. Horizontal move is applied directly to the variable
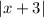
Up 2 units. Vertical move is applied to whole function
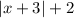
reflect obout the y-axis, we change the sign of the variable, then
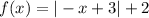
then right option is B
2.
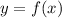
then -f(x) is -y
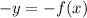
then change the value of -y
So the point must be on the graph of -f(x) is
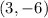
Then right option is D