Question

Emily, with a mass of 54.1 kilograms, is riding a wagon of mass 15.0 kilograms with a velocity of +4.12 meters per second. She then jumps off the wagon and lands on the ground with a horizontal velocity of +5.59 meters per second. What is the velocity of the wagon after Emily jumps off? Answer must be in 3 significant digits.

Answer 1

The initial momentum of the system can be expressed as,

`p_i=(m_1+m_2)u`

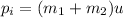
The final momentum of the system can be expressed as,

`p_f=m_1v_1+m_2v_2`

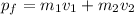
According to conservation of momentum,

`p_i=p_f`

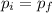
Plug in the known expressions,

`\begin{gathered} (m_1+m_2)u=m_1v_1+m_2v_2 \\ m_2v_2=(m_1+m_2)u-m_1v_1 \\ v_2=((m_1+m_2)u-m_1v_1)/(m_2) \end{gathered}`

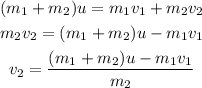
Substitute the known values,

`\begin{gathered} v_2=\frac{(54.1\text{ kg+15.0 kg)(4.12 m/s)-(54.1 kg)(5.59 m/s)}}{15.0\text{ kg}} \\ =\frac{284.692\text{ kgm/s-}302.419\text{ kgm/s}}{15.0\text{ kg}} \\ =-\frac{17.727\text{ kgm/s}}{15.0\text{ kg}} \\ =-1.18\text{ m/s} \end{gathered}`

Thus, the final velocity of wagon is -1.18 m/s where negative indicates that the wagon moves in the opposite direction.