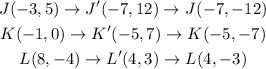Question

Triangle JKL has vertices J (-3, 5), K (-1, 0) and L (8, -4). Which of the following represents the translation of triangle JKL along vector <-4, 7> and its reflection across the x-axis?

Answer 1

Step-by-step explanation:

We are given a triangle with the vertices as shown below;

`\begin{gathered} J=(-3,5) \\ K=(-1,0) \\ L=(8,-4) \end{gathered}`

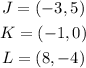
To translate along the vector,

`<-4,7>`

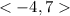
We shall apply the following rule;

`(x,y)\Rightarrow(x-4,y+7)`

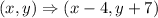
Therefore, for the points given, a translation along the vector (-4, 7) would be;

`\begin{gathered} J(-3,5)\Rightarrow(-3-4,5+7) \\ J^(\prime)=(-7,12) \end{gathered}`
`\begin{gathered} K(-1,0)\Rightarrow(-1-4,0+7) \\ K^(\prime)=(-5,7) \end{gathered}`
`\begin{gathered} L(8,-4)\Rightarrow(8-4,-4+7) \\ L^(\prime)=(4,3) \end{gathered}`

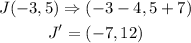
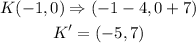
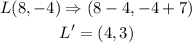
Now we have the new points as;

`\begin{gathered} J^(\prime)(-7,12) \\ K^(\prime)(-5,7) \\ L^(\prime)(4,3) \end{gathered}`

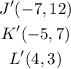
Next we shall reflect this shape across the x-axis.The rule for reflecting across the x-axis is given as;

`(x,y)\Rightarrow(x,-y)`

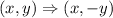
Imagine folding the graph page across the horizontal line (x-axis). That way, the x coordinate would still remain but the y coordinate would flip over from top to bottom or bottom to top.

Therefore, with the new coordinates we've determined, a reflection across the x-axis would become;

`\begin{gathered} J^(\prime)(-7,12)\Rightarrow(-7,-12) \\ J^(\doubleprime)(-7,-12) \end{gathered}`
`\begin{gathered} K^(\prime)(-5,7)\Rightarrow(-5,-7) \\ K^(\doubleprime)(-5,-7) \end{gathered}`
`\begin{gathered} L^(\prime)(4,3)\Rightarrow(4,-3) \\ L^(\doubleprime)(4,-3) \end{gathered}`

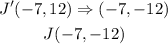
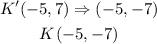
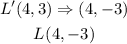
The new coordinates after the translation and the reflection would now be;

ANSWER:

`\begin{gathered} J(-3,5)\rightarrow J^(\prime)(-7,12)\rightarrow J^(\doubleprime)(-7,-12) \\ K(-1,0)\rightarrow K^(\prime)(-5,7)\rightarrow K^(\doubleprime)(-5,-7) \\ L(8,-4)\rightarrow L^(\prime)(4,3)\rightarrow L^(\doubleprime)(4,-3) \end{gathered}`