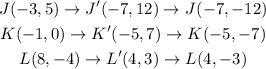Step-by-step explanation:
We are given a triangle with the vertices as shown below;

To translate along the vector,
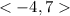
We shall apply the following rule;

Therefore, for the points given, a translation along the vector (-4, 7) would be;
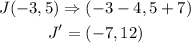
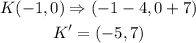
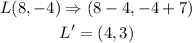
Now we have the new points as;
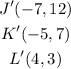
Next we shall reflect this shape across the x-axis.The rule for reflecting across the x-axis is given as;
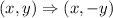
Imagine folding the graph page across the horizontal line (x-axis). That way, the x coordinate would still remain but the y coordinate would flip over from top to bottom or bottom to top.
Therefore, with the new coordinates we've determined, a reflection across the x-axis would become;
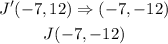
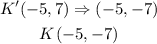
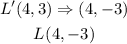
The new coordinates after the translation and the reflection would now be;
ANSWER: