Question

N is a rational number.m is an irrational number.n2 cannot be an irrational number? why or why not

Answer 1

If n is rational, it means that

`n\in\mathbb{Q}\Rightarrow n=(p)/(q),\quad p\in\mathbb{Z},\quad q\in\mathbb{Z}^*`

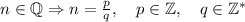
Therefore when we do n² we can write it as

`n^2=(p^2)/(q^2),\quad p\in\mathbb{Z},\quad q\in\mathbb{Z}^*`

Remember that the product of two integer numbers is also an integer, therefore we can guarantee that

`p^2\in\mathbb{Z}\text{ and }q^2\in\mathbb{Z}^*`

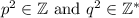
Then we can confirm that n² is the quotient of two integers and the denominator is not zero, therefore, n² is always rational, it cannot be an irrational number