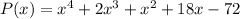Question

I need help with this question please. Ignore the wording below. Fyi this is a part of a homework practice

Answer 1

So,

Given that the zeros of our polynomial function are:

`3i,2,-4`

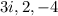
We know that there are 2 real zeros, and 2 complex zeros. (3i and -3i).

So, what we're going to do to find the equation of this polynomial, is to multiply all zeros together, such that we obtain an expression that we can simplify. Like this:

`(x-2)(x+4)(x-3i)(x+3i)`

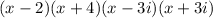
Now, we're going to multiply and distribute:

`\begin{gathered} (x^2+2x-8)(x^2+3xi-3xi-9i^2) \\ \to(x^2+2x-8)(x^2-9i^2) \end{gathered}`

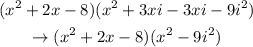
Remember that:

`i=\sqrt[]{-1}\to i^2=-1`

So, we can rewrite:

`(x^2+2x-8)(x^2+9)`

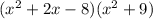
Multiplying these terms, we got that:

`\begin{gathered} (x^2+2x-8)(x^2+9) \\ \to x^4+9x^2+2x^3+18x-8x^2-72 \\ \to x^4+2x^3+x^2+18x-72 \end{gathered}`

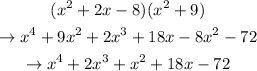
Therefore,

`P(x)=x^4+2x^3+x^2+18x-72`