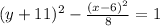The standard form of the equation of the hyperbola is
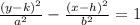
(h, k) are the coordinates of the center
(h, k + a), (h, k - a) are the vertices
(h, k + c), (h, k - c) are the foci
Since the foci are (6, -8), (6, -14), then

Since the vertices are (6, -10), (6, -12), then
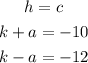
To find k we will add the equations of k and a, or k and c
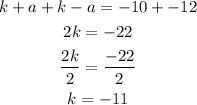
Substitute the value of k in the equation of foci to find and vertices to find a and c
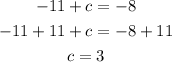
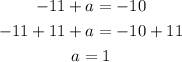
To find b we will use the equation

Since a = 1 and c = 3, then
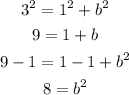
Substitute the value of h, k, a^2, b^2 in the form of the equation above
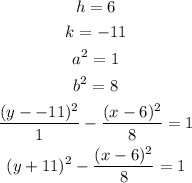
The equation of the hyperbola in the standard form is