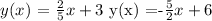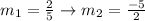If we have the equation of the from

Then a line perpendicular to that equation is
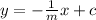
Let us bring each of the lines in slope-intercept form.
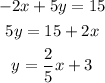
The other equation in slope-intercept form is
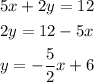
As we can see the second equation is negative of the reciprocal of the second equation; therefore, the two lines are perpendicular.