Question

PLESS I DONT WANT TO GET BEAT TODAY BY MY MOM PLESSSS HELP ME х у х Note: Figure is not drawn to scale. If x = 5 units, y = 15 units, and h = 8 units, find the area of the parallelogram shown above using decomposition.

Answer 1

We can decomposite the parallelogram into two right triangles and one rectangle. To find the total area we have to calculate the area of each figure and add them.

• Area of the right triangles (At):

`A_t=2\cdot(x* h)/(2)`

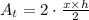
where the first number 2 represents the two triangles, x represents the base of the triangles and h the height. Solving for At:

`A_t=x* h=5*8=40units^2`

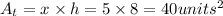
• Area of rectangle (Ar):

`A_r=y* h`

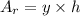
where y represents the base of the rectangle and h represents the height of the rectangle. Solving for Ar:

`A_r=15*8=120units^2`

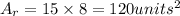
Finally, finding the area of the parallelogram (Ap):

`A_p=A_t+A_r=40+120=160units^2`

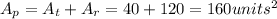
Answer: 160 units²