The given function is:
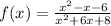
Vertical asymptotes occur when the denominator of the function is equal to zero.
The denominator can be factored and rewritten as:

The numerator also can be factored and rewritten as:
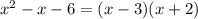
Then the function is:
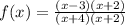
Simplify (x+2)/(x+2):
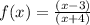
Equal the denominator to zero and find the x-value that make the function undefined:
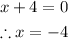
There is a horizontal asymptote at x=-4.
The horizontal asymptotes occur when:
- The degree of the numerator is less than the degree of the denominator or
- The degree of the numerator is equal to the degree of the denominator.
In this case, the degree of the numerator is 2 and the degree of the denominator is 2, then they are equal. The horizontal asymptote, in this case, is at:
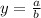
Where a is the leading coefficient in the numerator and b is the leading coefficient in the denominator.
The leading coefficient in the numerator is 1, and the leading coefficient in the denominator is 1. Then the horizontal asymptote is at y=1:
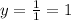
Also, the function at x=-2.1 is:

Answer: As can be seen, the function that matches with the asymptotes and f(-2.1)=-2.7 is the first graph.