Question

Hello! It’s Rose I need help with this practice problem I will include another picture with the rest of the answer options (total of four answer options to the problem)

Answer 1

The given function is:

`f(x)=(x^2-x-6)/(x^2+6x+8)`

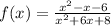
Vertical asymptotes occur when the denominator of the function is equal to zero.

The denominator can be factored and rewritten as:

`x^2+6x+8=(x+4)(x+2)`

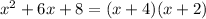
The numerator also can be factored and rewritten as:

`x^2-x-6=(x-3)(x+2)`

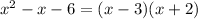
Then the function is:

`f(x)=((x-3)(x+2))/((x+4)(x+2))`

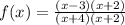
Simplify (x+2)/(x+2):

`f(x)=((x-3))/((x+4))`

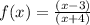
Equal the denominator to zero and find the x-value that make the function undefined:

`\begin{gathered} x+4=0 \\ \therefore x=-4 \end{gathered}`

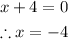
There is a horizontal asymptote at x=-4.

The horizontal asymptotes occur when:

- The degree of the numerator is less than the degree of the denominator or

- The degree of the numerator is equal to the degree of the denominator.

In this case, the degree of the numerator is 2 and the degree of the denominator is 2, then they are equal. The horizontal asymptote, in this case, is at:

`y=(a)/(b)`

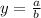
Where a is the leading coefficient in the numerator and b is the leading coefficient in the denominator.

The leading coefficient in the numerator is 1, and the leading coefficient in the denominator is 1. Then the horizontal asymptote is at y=1:

`y=(1)/(1)=1`

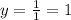
Also, the function at x=-2.1 is:

`\begin{gathered} f(-2.1)=((-2.1)^2-(-2.1)-6)/((-2.1)^2+6(-2.1)+8) \\ f(-2.1)=(4.41+2.1-6)/(4.41-12.6+8) \\ f(-2.1)=(0.51)/(-0.19) \\ f(-2.1)=-2.7 \end{gathered}`

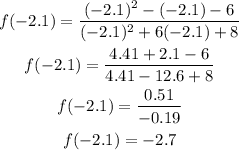
Answer: As can be seen, the function that matches with the asymptotes and f(-2.1)=-2.7 is the first graph.