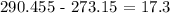Answer:
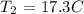
Step-by-step explanation:
Here, we want to get the initial temperature
From Charles' law, we know that at constant pressure, the volume of a given mass of gas is directly proportional to its temperature
Mathematically, we can have this written as:
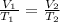
We can rewrite the formula in terms of the missing value as follows:
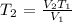
Let us write out the values given, not forgetting that we have to convert the temperature value to Kelvin by adding 273.15 K
Thus, we have:
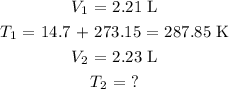
Substituting these values in the re-written formula, we have it as:
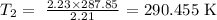
Finally, what we have to do is to convert this temperature to degrees celsius by subtracting 273.15 K
We have this as: