Given:
The 5th term of an arithmetic progression is 20.
The 12th term of an arithmetic progression 41.
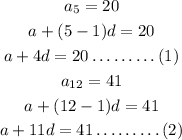
a) To find the common difference:
Subtract equation (1) from (2), we get
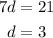
Hence, the common difference is 3.
b) To find the first term:
Substitute d=3 in equation (1), we get
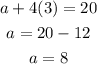
Hence, the first term is 8.
c) To find the sum of the first 8 terms:
Using the sum formula,

Hence, the sum of the first 8 terms is 148.