Given:
We have height of Brian is 6 ft, Brian is standing 10.7 ft from the mirror, mirror is 37 ft from the tree.
Required:
We need to find the height of tree.
Step-by-step explanation:
Here triangle ABC and triangle EDC are similar triangles
so we can also apply that
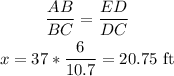
Final answer:
The tree is 20.75 ft tall.