Given equation:
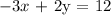
The y-intercept
The y-intercept can be found by substituting 0 for x and then solving for y:
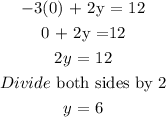
Answer: (0,6)
The x-intercept
The x-intercept can be found by substituting 0 for y and then solving for x
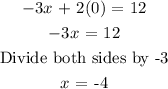
Answer: (-4,0)
the slope
The slope can be found by re-writing the equation in slope-intercept form:
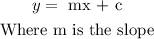
Hence:
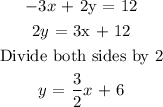
Answer:
slope = 3/2
The graph of the line can be obtained by joining two points using a straight line.
We have the points (0,6) and (-4,0)
Hence, the graph of the line is: