Question

A cashier has a total of 134 bills, made up of fives and tens. The total value of the money is $790. How many ten-dollar bills does the cashier have?

Answer 1

Let:

F be the number of five-dollar bills.

T be the number of ten-dollar bills.

Then, follow the steps to find T.

Step 01: Write an equation that represents the total number of bills.

Since 134 is the sum of the bills of five and ten dollars:

`F+T=134`

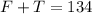
Step 02: Write an equation that represents the amount of money the cashier has.

The cashier has $790 dollar, which is equal to F multiplied by 5 plus T multiplied by 10:

`790=5\cdot F+10\cdot T`

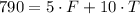
Step 02: Isolate F in the equation from step 01 and substitute it in equation from step 02.

To isolate F, subtract T from both sides.

`\begin{gathered} F+T-T=134-T \\ F=134-T \end{gathered}`

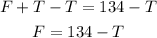
And substituting it in the second equation:

`790=5\cdot(134-T)+10\cdot T`

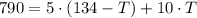
Step 03: Solve the equation from step 02 for T.

`\begin{gathered} 790=5\cdot134-5\cdot T+10\cdot T \\ 790=670+5\cdot T \end{gathered}`

Subtract 670 from both sides, then divide the sides by 5.

`\begin{gathered} 790-670=670+5\cdot T-670 \\ 120=5\cdot T \\ (120)/(5)=(5)/(5)\cdot T \\ 24=T \end{gathered}`

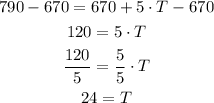
Step 04: Knowing T, find F using the equation from Step 02.

`\begin{gathered} F=134-T \\ F=134-24 \\ F=110 \end{gathered}`

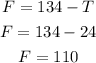
Answer:

He has 24 ten-dollar bills.