This problem deals with an exponential decay process. The general equation describing a decay is written as
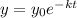
where y0 represents the initial state of the system and k is the decay constant.
In the given problem, we have y0 = 157. After t =4, the value of y becomes 18. We will be using these values to solve first the decay constant of the problem. We have
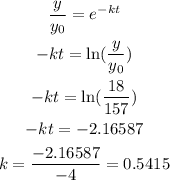
We use this decay constant to solve the number of bank failures in 2018. In the year 2018, t = 8. Hence, the number of bank failures at this time will be
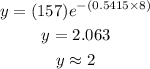
There will be 2 bank failures in 2018.