Question

Consider the following graph of two functionsStep 2: Find (g-f)(-5)Step 3: Find (g.f)(1)Step 4: Find (f/g)(-3)

Answer 1

• (g-f)(-5)=16

,

• (g.f)(-1)=-16

,

• (f/g)(-3)=-1

Explanation:

Given the graph of f(x) and g(x):

Part 2

• When x=-5, f(x)=-8.

,

• When x=-5, g(x)=8

Thus:

`\begin{gathered} f(-5)=-8 \\ g(-5)=8 \end{gathered}`

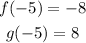
The composition of the functions:

`\begin{gathered} (g-f)(-5)=g(-5)-f(-5) \\ =8-(-8) \\ =8+8 \\ \implies(g-f)(-5)=16 \end{gathered}`

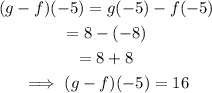
The answer is 16.

Part 3

• When x=1, f(x)=4.

,

• When x=1, g(x)=-4

Therefore:

`\begin{gathered} f(1)=4 \\ g(1)=-4 \\ \implies(g\cdot f)(-1)=(g)(-1)\cdot(f)(-1) \\ =-4*4 \\ =-16 \end{gathered}`

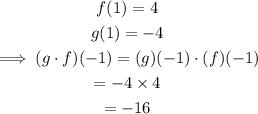
The answer is -16.

Part 4

• When x=-3, f(x)=-4.

,

• When x=-3, g(x)=4

Therefore:

`\begin{gathered} f(-3)=-4 \\ g(-3)=4 \end{gathered}`

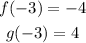
The composition is calculated below:

`((f)/(g))(-3)=(f(-3))/(g(-3))=-(4)/(4)=-1`

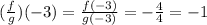
The answer is -1.