Answer:
• (g-f)(-5)=16
,
• (g.f)(-1)=-16
,
• (f/g)(-3)=-1
Explanation:
Given the graph of f(x) and g(x):
Part 2
• When x=-5, f(x)=-8.
,
• When x=-5, g(x)=8
Thus:
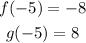
The composition of the functions:
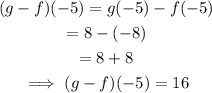
The answer is 16.
Part 3
• When x=1, f(x)=4.
,
• When x=1, g(x)=-4
Therefore:

The answer is -16.
Part 4
• When x=-3, f(x)=-4.
,
• When x=-3, g(x)=4
Therefore:
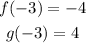
The composition is calculated below:
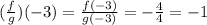
The answer is -1.