Question

A research institute poll asked respondents if they felt vulnerable to identity theft. In the poll, n=1086 and x=571 who said "yes." Use a 99% confidence level. A. find the best point of estimate of the population of portion p.B. Identify the value of the margin of error E.E= round to four decimal places as needed.C. Construct the confidence interval._ < p <_ round to three decimal places.

Answer 1

Given:

`\begin{gathered} n=1086 \\ x=571 \end{gathered}`

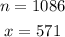
To Determine: Using 99% confidence interval, the best point of estimate of the population of portion p

Solution

`\begin{gathered} Point-of-estimation(PE)=(x)/(n) \\ PE=(571)/(1086) \\ PE=0.5258 \end{gathered}`

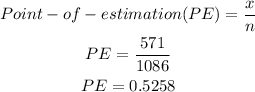
The formula for finding the margin of error is

`MOE=\sqrt{(0.5258*(1-0.5258))/(1086)}* z`
`\begin{gathered} MOE=\sqrt{(0.24933436)/(1086)}* z \\ MOE=0.01515* z \end{gathered}`

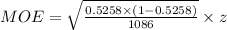
The z score corresponding to 99% confidence interval from the table is 2.575

Therefore

`\begin{gathered} MOE=0.01515*2.575 \\ MOE=0.039 \end{gathered}`

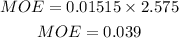
Hence

A. Point of estimation of the population of portion p is approximately 0.5258 (4 decimal places) OR 0.526(3 decimal places)

B. The margin of Error is apprimately 0.039