Given
J(2, -7) ; K(-6, -2) ; L(-1, 6) ; M(7, 1 )
Find
Length of KL and length of side adjacent to KL
Step-by-step explanation
by distance formula we find the length of sides.
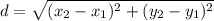
so ,
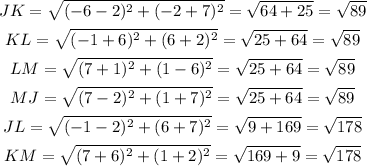
here all sides are equal and diagonal are equal , so it is a square .
a) Length of KL and length of side adjacent to KL is
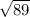
slope of KL is given by
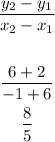
slope of side adjacent to KL is given by
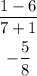
Final Answer
a) Length of KL and side adjacent to KL is
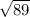
b) Slope of KL = 8/5
slope of side adjacent to KL is -5/8
c) it is a sqaure.