Given:
The cost of a ticket to the circus is $15.00 for children and $37.00 for adults. On a certain day, attendance at the circus was 900 and the total gate revenue was $24,500.
Required:
We need to find that how many childern and adults were there
Step-by-step explanation:
Consider number of children as x and number of adults as y
so by attendance at the circus was 900 we can say that and call that equation as 1
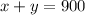
and by cost of a ticket to the circus is $15.00 for children and $37.00 for adults and total revenue was $24,500 we can say that and called that equation as 2
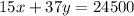
now multiply eq 1 with 15 and thn substract from eq 2
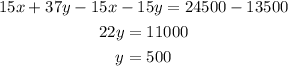
substitute the value of y in eq 1 to find the x
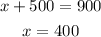
Final answer:
The number of children was 400 and the number of adult was 500