Question

Rebecca has 12 photos she wants to hang side by side on her wall.A. If she only wants to display 8 of the photos, in how many ways can she choose 8 photos she wishes toeventually display? Show your work.B.In how many ways can she arrange all 12 photos? Show your work.c. If Rebecca wants to have the 10 out of 12 photos in specific places, how many ways could she order the12 photos? Show your work.

Answer 1

A.

If she will choose 8 from 12 photos, the total number of ways she can choose is given by a combination of 12 choose 8, since the order of the photos doesn't matter.

The formula for a combination of n choose p is:

`C(n,p)=(n!)/(p!(n-p)!)`

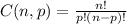
For n = 12 and p = 8, we have:

`C(12,8)=\frac{12!}{8!(12-8)!_{}}=(12\cdot11\cdot10\cdot9\cdot8!)/(8!\cdot4!)=(12\cdot11\cdot10\cdot9)/(4\cdot3\cdot2)=495`

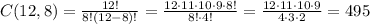
So there are 495 ways.

B.

If she wants to arrange the 12 photos, the total number of ways is given by the factorial of 12:

`12!=12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2=479001600`

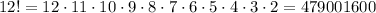
There are 479,001,600 ways.

C.

Since 10 photos already have specific places, we need to calculate the number of ways to arrange the other two photos in the two remaining places.

In this case, there are only 2 ways of organizing the remaining two photos:

Photo 1 first, photo 2 last, or photo 1 last and photo 2 first.