Convert the equation into vertex form, then solve the equation x^2 + 6x + 8 = 0

Question

asked Jan 12, 2023 168k views

1 Answer

Tim Anishere · Answer 1 · 2023-01-19T02:25:24+0000

The Vertex form of a Quadratic function is:

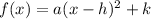
$f(x)=a\mleft(x-h\mright)^2+k$

Where the vertex of the paraboola is:

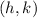
Given the following Quadratic equation:

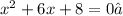
You need to convert it into Vertex form by completing the square. The steps are shown below:

- Identify the coefficient of the term with the variable "x". In this case, this is:

- Divide it by 2 and square it:

- Add and subtract the number obtained (in the right side of the equation):

- Order it and express it as a square of a binomial, you get:

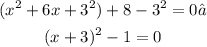
$\begin{gathered} (x^2+6x+3^2)+8-3^2=0 \\ (x+3)^2-1=0 \end{gathered}$

- Add 1 to both sides of the equation:

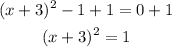
$\begin{gathered} (x+3)^2-1+1=0+1 \\ (x+3)^2=1 \end{gathered}$

To solve the equation you must take the square root of both sides of the equation:

$\begin{gathered} \sqrt[]{(x+3)^2}=\pm\sqrt[]{1} \\ \\ x+3=\pm1 \end{gathered}$

Finally, subtract 3 from both sides of the equation:

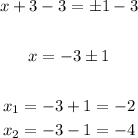
$\begin{gathered} x+3-3=\pm1-3 \\ \\ x=-3\pm1 \\ \\ x_1=-3+1=-2 \\ x_2=-3-1=-4 \end{gathered}$

The answer is:

- Vertex form:

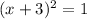
- Solutions:

$\begin{gathered} x_1=-2 \\ x_2=-4 \end{gathered}$