Question

Find the equation of the line in slope-intercept form.Parallel to: 6x+2y=1 Passing through: (-3,2)

Answer 1

`y=-3x-7`

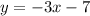
Step-by-step explanation

We want to find the equation of the line passing through (-3, 2) and parallel to:

`6x+2y=1`

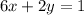
First, put the equation in slope intercept form:

`\begin{gathered} 2y=-6x+1 \\ y=-3x+(1)/(2) \\ \text{where slope, m = -3} \\ in\text{tercept, b = }(1)/(2) \end{gathered}`

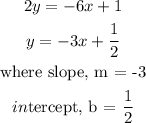
A line that is parallel to another line has the same slope as that line.

Therefore, the slope of the required line is -3.

Now, use the point-slope method to find the equation of the line:

`y-y1=m(x-x1)`

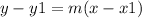
where (x1, y1) is the point the line passes through

Therefore, the equation of the line is:

`\begin{gathered} y-2=-3(x-(-3)) \\ y-2=-3(x+3) \\ y-2=-3x-9 \\ \Rightarrow y=-3x-9+2_{} \\ y=-3x-7 \end{gathered}`

That is the equation of the line.