Third leg.
The crew flies at a speed of 560 mi/h in direction N-20°-E.
The wind has a speed of 35 mi/h and a direction S-10°-E.
We then can draw this as:
We have to add the two vectors to find the actual speed and direction.
We will start by adding the x-coordinate (W-E axis):

and the y-coordinate (S-N axis) is:
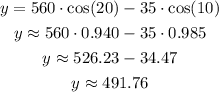
Then, the actual speed vector is v3=(197.61, 491.76).
The starting location for the third leg is R2=(216.66, 167.67) [taken from the previous answer].
Then, we have to calculate the displacement in 20 minutes using the actual speed vector.
We can calculate the movement in each of the axis. For the x-axis:
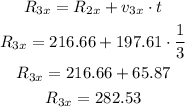
NOTE: 20 minutes represents 1/3 of an hour.
We can do the same with the y-coordinate:
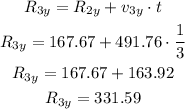
The final position is R3 = (282.53, 331.59).
To find the distance from the origin and direction, we transform the cartesian coordinates of R3 into polar coordinates:
The distance can be calculated as if it was a right triangle:
![\begin{gathered} d^2=x^2+y^2_{} \\ d^2=282.53^2+331.59^2 \\ d^2=79823.20+109951.93 \\ d^2=189775.13 \\ d=\sqrt[]{189775.13} \\ d\approx435.63 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dr3qe7lnbosrw0ok5da1rpd8kxsho3i43q.png)
The angle, from E to N, can be calculated as:
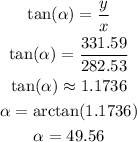
If we want to express it from N to E, we substract the angle from 90°:
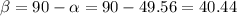
Answer: the final location can be represented with the vector (282.53, 331.59).
1) The distance from the origin is 435.63 miles and
2) the direction is N-40°-E.