Question

Water flows through a 4.50-cm inside diameter pipe with a speed of 12.5 m/s. At a later position, the pipe has a 6.25-cm inside diameter. Determine the flow speed (in m/s) at the second point in the pipe. Assume that the water acts as an ideal fluid.

Answer 1

Given,

The initial inside diameter of the pipe, d₁=4.50 cm=0.045 m

The initial speed of the water, v₁=12.5 m/s

The diameter of the pipe at a later position, d₂=6.25 cm=0.065 m

From the continuity equation,

`\begin{gathered} A_1v_1=A_2v_2 \\ \pi((d_1)/(2))^2v_1=\pi((d_2)/(2))^2v_2 \\ \Rightarrow d^2_1v_1=d^2_2v_2 \end{gathered}`

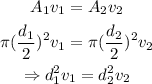
Where A₁ is the area of the cross-section at the initial position, A₂ is the area of the cross-section of the pipe at a later position, and v₂ is the flow rate of the water at the later position.

On substituting the known values,

`\begin{gathered} 0.045^2*12.5=0.065^2* v_2 \\ \Rightarrow v_2=(0.045^2*12.5)/(0.065^2) \\ =5.99\text{ m/s} \end{gathered}`

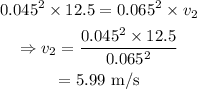
Thus, the flow rate of the water at the later position is 5.99 m/s