154.03 m/s
Step-by-step explanationThe Pythagorean theorem states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)

so, to add the vectors we solve use tht P.T and solve for c
s
Step 1
a) let

b) now, replace in the formula:
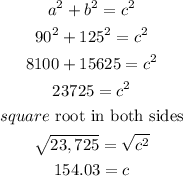
therefore, the answer is
154.03 m/s
I hope this helps you