Question

Given the function h(x)=x^2-8x+8, determine the average rate of change of the function over the interval 2≤x≤9.

Answer 1

The rule of the average rate of a function f(x) on the interval [a, b] is

`R=(f(b)-f(a))/(b-a)`

Since the given function is

`f(x)=x^2-8x+8,2\leq x\leq9`

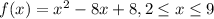
Then put a = 2 and b = 9, then find f(2) and f(9), and substitute them in the rule above.

`\begin{gathered} f(2)=(2)^2-8(2)+8 \\ f(2)=4-16+8 \\ f(2)=-4 \end{gathered}`
`\begin{gathered} f(9)=(9)^2-8(9)+8 \\ f(9)=81-72+8 \\ f(9)=17 \end{gathered}`

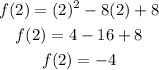
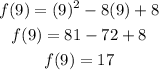
Substitute the values of a, b, f(a), and f(b) in the rule above

`\begin{gathered} R=(17--4)/(9-2) \\ \\ R=(17+4)/(7) \\ \\ R=(21)/(7) \\ \\ R=3 \end{gathered}`

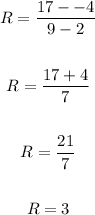
The average rate of change on the given interval is 3