We are asked to determine a set of parametric equations for the parabolic motion of an object. The parametric equations for such a motion is given by:
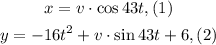
To determine the velocity we will solve for "t" in equation (1):
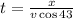
Now, we will replace this in equation (2):
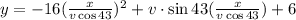
Simplifying:
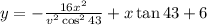
Now we replace the values x = 54.5 and y = 0:
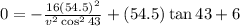
Simplifying:
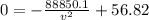
Now we solve for "v":
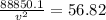
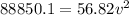
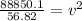
Solving the operation:
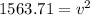
taking the square root:
![\begin{gathered} \sqrt[]{1563.71}=v \\ 39.54=v \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/mhqs5p6r9x8h6ltdd9o13zfk5iy8rxlw9l.png)
Therefore, the velocity is 39.54 ft/s.