The probability that event B occurs is 1/4
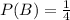
The probability that event A occurs given that event B occurs is 1/3
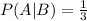
What is the probability that events A and B both occur?
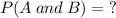
Recall that the conditional probability is given by
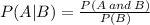
Re-writing the above formula for P(A and B)

So, the probability that events A and B both occur is
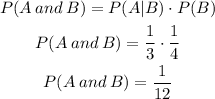
Therefore, the probability that events A and B both occur is 1/12