Question

Assume no loss of energy to friction. If a 270 kg roller coaster is 96.8 meters tall and has an initial velocity of zero, what will the velocity be at the bottom?

Answer 1

43.56 m/s

Step-by-step explanation

Given:

• The roller coaster's mass, m = 270 kg

,

• The roller coaster's height, h = 96.8 m

,

• The roller coaster's initial velocity, v₀ = 0 m/s

Unknown:

• The roller coaster's final velocity at the bottom of the hill, v

By the law of conservation of energy, the total mechanical energy of the roller coaster at the top of the hill must be equal to its total mechanical energy at the bottom. If no energy is lost to friction, then we only have gravitational potential energy and kinetic energy,

`PE_o+KE_o=PE_f+KE_f`

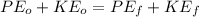
The height where the roller coaster starts its motion is with respect to the bottom of the hill. This means that at the bottom of the hill, we could say that its height is zero and, therefore, it has no gravitational potential energy.

Also, we know that the roller coaster starts from rest, so its initial kinetic energy is zero. The equation above reduces to,

`PE_o=KE_f`

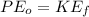
Replace with the expressions for each of these kinds of energy,

`m\cdot g\cdot h=(1)/(2)\cdot m\cdot v^2`

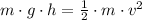
The mass is on both sides of the equality, so it cancels out,

`g\cdot h=(1)/(2)v^2`

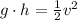
Solving for v,

`v=\sqrt[]{2\cdot g\cdot h}`

Replace with the known values. The acceleration due to gravity is 9.8 m/s,

`v=\sqrt[]{2\cdot9.8m/s\cdot96.8m}\approx43.56m/s`

Hence, the velocity of the roller coaster at the bottom is 43.56 m/s.