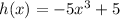Question

Identify the function that relects f(x)=5x^3-3 across the x-axis and shifts it 2 units up.

Answer 1

To find the new function, follow the steps below.

Step 01: Reflect the function over the x-axis.

After reflecting the function f(x) over the x-axis, the new function is -f(x).

Then:

`\begin{gathered} f(x)=5x^3-3 \\ -f(x)=-(5x^3-3) \\ -f(x)=-5x^3+3 \end{gathered}`

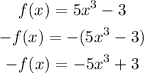
Step 02: Shift the function 2 units up.

When the function is shifted n units up, the new function if f(x) + n.

The,

`\begin{gathered} h(x)=-f(x)+2 \\ h(x)=-5x^3+3+2 \\ h(x)=-5x^3+5 \end{gathered}`

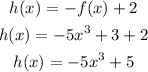
Answer:

`h(x)=-5x^3+5`