ANSWER
-3
Step-by-step explanation
The formula for the general term of a geometric sequence is:
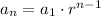
In this sequence the first term a1 = -2. With this and the second term a2 = 6 we can find the common ratio and then verify with the next terms:
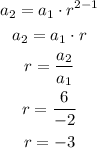
If we use this common ratio to find the 3rd and 4th terms we have to arrive to the same result as the given sequence:
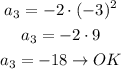
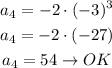
The common ratio of this sequence is -3